时间复杂度是什么？

• 一个函数，用大O表示，比如O（1）、O（n）、 O（logN）...
• 定性描述该算法的运算时间
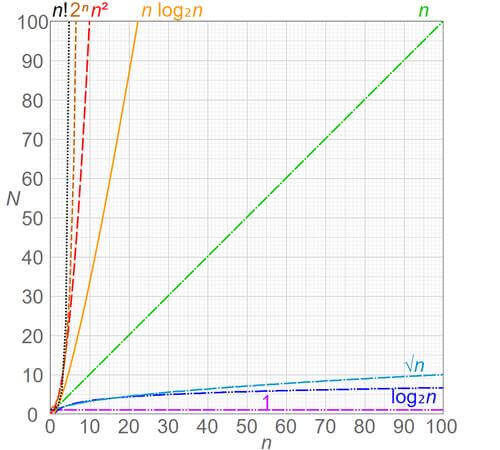
• 需要关注的 O(1) < O（log₂n）< O（n）< O（n²）

主要的时间复杂度有：

• 常数阶 O（1）：无论代码执行了多行，只要没有循环等复杂结构，那这个代码的复杂度就是 O(1)
• 对数阶 O（logN）：在while循环里面，每次都将 i 乘以 2，乘完之后，i 距离 n 就越来越近了。我们试着求解一下，假设循环x次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 x 次方等于 n，那么 x = log2(n)
  也就是说当循环 log2(n) 次以后，这个代码就结束了。因此这个代码的时间复杂度趋势为：O(logn)
• 线性阶 O(n)： 在 单层 循环体内，代码会随着每次循环执行，它消耗的时间是随着n的变化而变化的，因此这是一个线性相关趋势，时间复杂度为 O(n)。

• 线性对数阶 O(nlogN)：线性对数阶O(nlogN) 其实非常容易理解，将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了O(nlogN)。

  for (let i = 0; i < n; i++) {
       let m = 1;
    while(m < n) {
        i = i * 2;
    }
  }

• 平方阶 O(n^2)： 将 O(n) 的代码再循环嵌套一遍，它的时间复杂度就是 O(n^2)。

  for (let i = 0; i < n; i++) {
       for (let j = 0; i < n; i++) {
        console.log(i, j)
    }
  }

  如果将其中一层循环的n改成m，即：

  for (let i = 0; i < m; i++) {
       for (let j = 0; i < n; i++) {
        console.log(i, j)
    }
  }

那么它的时间复杂度就变成了 O(m*n)

• 立方阶 O(n^3)： O(n³)相当于三层n循环，其它的类似
• K次方阶 O(n^k)
• 指数阶 O(2^n)

空间复杂度是什么？

• 一个函数，用大O表示，比如O（1）、O（n）、O（n²）
• 算法在运行过程中临时占用存储空间大小的量度

常见空间复杂度：

• 空间复杂度 O(1)，如果算法执行所需要的临时空间不随着某个变量 n 的大小而变化，即此算法空间复杂度为一个常量，可表示为 O(1);

• 空间复杂度 O(n)

  const list = []
  for(let i = 0; i < n; i +=1 ){
    list.push(i);
  }

• 空间复杂度 O(n^2)

  const matrix = []
  for (let i = 0; i < n; i++) {
      matrix.push([]);
      for (let j = 0; i < n; j++) {
        matrix[i].push(j);
      }
  }

  开始定义了一个数组，而后使用 for 循环再次定义了一个数组，相当于创建了一个二维数组(矩阵)，这个数组中的每一项都是一个空间度量为 n 的数组，因此它的空间复杂度为 O(n^2)

阶段思考题：

1. 如果一段代码中有3个循环，它们的循环次数都是n，那么这段代码的时间复杂度是O（3n）还是O（n）？

   • 如果是 3 个并列循环的代码，那么总的时间复杂度趋势为 O(n)
   • 如果是 3 个循环嵌套，那么总的时间复杂度趋势为 O(n^3)

2. 假设每天睡觉前，你都会数2的次方，1、2、4、8...,每次你都数到n才能睡着，那么你数了几个数？时间复杂度是多少？

   • 数了：2^x = n ==> x = log2(n) ; x 从 0 算起 所以数了 log2(n) + 1 个数
   • 时间复杂度的趋势为 O(logN)