图是什么？

• 图是网络结构的抽象模型，是一组由边连接的节点
• 图可以表示任何二元关系，比如道路、航班。
• JS中没有图，但是可以用Object和Array构建图
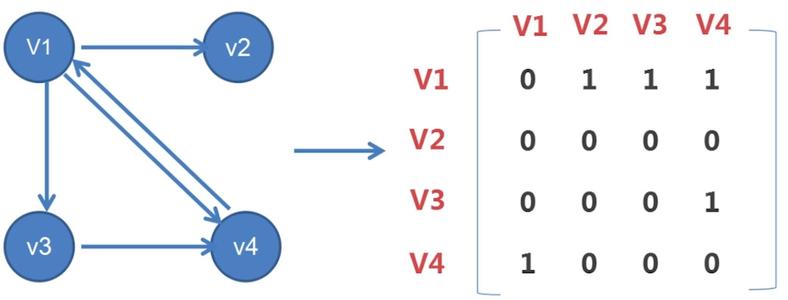
• 图的表示法：邻接矩阵，邻接表，关联矩阵

{
  "V1"：["V2", "V3", "V4"],
  "V2": [],
  "V3": ["V4"],
  "V4": ["V1"]
}

图的常用操作

• 深度优先遍历：尽可能深的搜索图的分支
• 广度优先遍历：先访问离根节点最近的节点

图的深度优先遍历的算法口诀

• 访问根节点
• 对根节点的没访问过的相邻节点挨个进行深度优先遍历

图的广度优先遍历的算法口诀

• 新建一个队列，把根节点入队
• 把队头出队并访问
• 把队头的没访问过的相邻节点入队
• 重复第二三步，直到队列为空

// graph.js
const graph ={
  0: [1, 2],
  1: [2],
  2: [0, 3],
  3: [3]
}
module.exports = graph;

// 图的深度优先遍历实现
const graph= require('./graph');
// 用来记录已访问过的节点
const visited = new Set();
const dfs = (n)=>{
  console.log(n);
  visited.add(n);
  graph[n].forEach(c => { // 拿到所有相邻节点
    if(!visited.has(c)){ // 还未访问过的相邻接点
      dfs(c);
    }
  });
};
dfs(2);

// 图的广度优先遍历实现
const graph = require('./graph')
const visited = new Set();
visited.add(2);
const queue = [2];
while(queue.length){
  const n = queue.shift();
  console.log(n);
  graph[n].forEach(c => {
    if(!visited.has(c)){
      queue.push(c);
      visited.add(c);
    }
  });
}

LeetCode #65 有效的数组

LeetCode #417 太平洋大西洋水流问题

给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界，而“大西洋”处于大陆的右边界和下边界。

规定水流只能按照上、下、左、右四个方向流动，且只能从高到低或者在同等高度上流动。

请找出那些水流既可以流动到“太平洋”，又能流动到“大西洋”的陆地单元的坐标。

提示：

• 输出坐标的顺序不重要
• m 和 n 都小于150
   

示例：

给定下面的 5x5 矩阵:

  太平洋 ~   ~   ~   ~   ~ 
       ~  1   2   2   3  (5) *
       ~  3   2   3  (4) (4) *
       ~  2   4  (5)  3   1  *
       ~ (6) (7)  1   4   5  *
       ~ (5)  1   1   2   4  *
          *   *   *   *   * 大西洋

• 返回：[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).

解题思路：

1. 把矩阵想象成图（有向图）
2. 从海岸线逆流而上遍历图，所到之处就是可以流到某个大洋的坐标
   解题步骤：
3. 新建两个矩阵，分别记录能流到两个大洋的坐标
4. 从海岸线，多管齐下，同时深度优先遍历图，过程中填充上边的那个矩阵
5. 遍历两个矩阵，找出能流到两个大洋的坐标

复杂度：

1. 时间复杂度O（m * n）
2. 空间复杂度O（m * n）

/**
 * @param {number[][]} matrix
 * @return {number[][]}
 */
var pacificAtlantic = function(matrix) {
    if(!matrix || !matrix[0]){
        return [];
    }
    const m = matrix.length;
    const n = matrix[0].length;
    // 构建数组的两种方法1. Array.from({length:n}) 2. new Array(n)
    const flow1 = Array.from({length: m}, ()=> {return new Array(n).fill(false)});  // 能流到太平洋的矩阵
    const flow2 = Array.from({length: m}, ()=> {return new Array(n).fill(false)}); // 能流到大西洋的矩阵
    const dfs = (row, cow, flow)=>{ // 行，列
        flow[row][cow] = true;
        [[row-1, cow], [row+1, cow], [row, cow-1], [row, cow+1]].forEach(([nextrow, nextcow])=>{ 
          // 相邻的上，下，左，右四个节点的数组遍历
            if(
                //保证下一个节点在矩阵中
                nextrow >= 0 && nextrow < m  &&
                nextcow >= 0 && nextcow < n  &&
                // 防止死循环，即保证未访问过该节点
                !flow[nextrow][nextcow] && 
                // 保证逆流而上
                matrix[nextrow][nextcow] >= matrix[row][cow]
            ){ 
                dfs(nextrow, nextcow, flow)
            }
        })
    };
    // 沿着海岸线逆流而上
    for(let row=0; row<m; row++){
        dfs(row, 0 ,flow1); // 从第一行到最后一行，保证第一列，流到太平洋
        dfs(row, n-1, flow2); // 遍历最后一列的格子，流到大西洋 传flow2
    }
    for(let cow=0; cow<n; cow++){
        dfs(0, cow, flow1); // 遍历第一行，太平洋
        dfs(m-1, cow, flow2); // 遍历最后一行，大西洋
    }
    // 收集能流到两个大洋的坐标
    const res = [];
    for(let row=0; row<m; row++){ // 遍历所有行
        for(let cow=0; cow<n; cow++){ // 遍历所有列
            if(
                flow1[row][cow] && // 能流到太平洋
                flow2[row][cow] // 能流到大西洋
            ){
                res.push([row,cow])
            }
        }
    }
    
    // console.log(flow1)
    // console.log(flow2)
    return res;
};

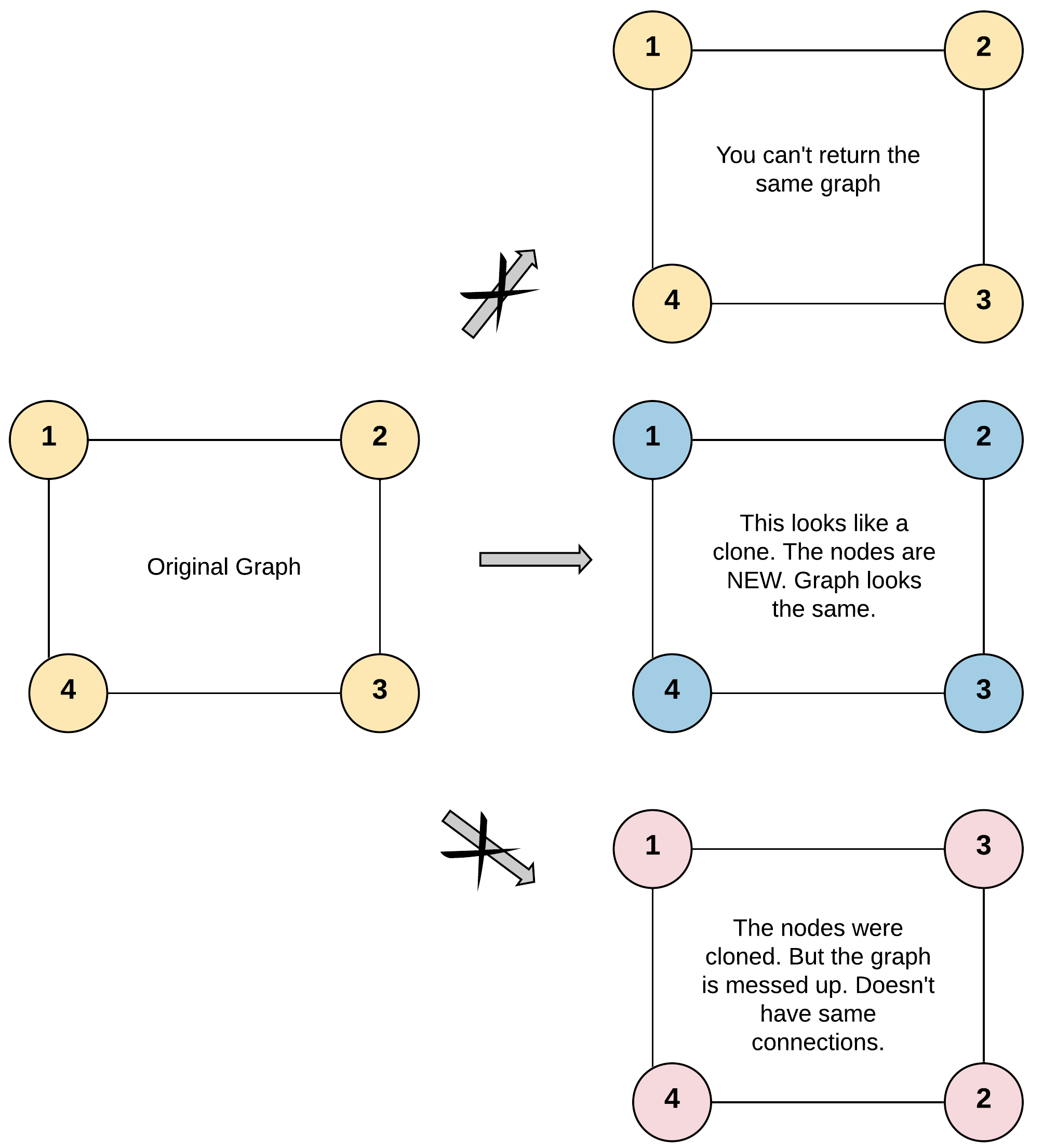
LeetCode #133 克隆图

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

示例1：

输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

• 输入：adjList = [[]]
• 输出：[[]]
• 解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例3：

• 输入：adjList = []
• 输出：[]
• 解释：这个图是空的，它不含任何节点。

示例4：

• 输入：adjList = [[2],[1]]
• 输出：[[2],[1]]
   

提示：

节点数不超过 100 。
每个节点值 Node.val 都是唯一的，1 <= Node.val <= 100。
无向图是一个简单图，这意味着图中没有重复的边，也没有自环。
由于图是无向的，如果节点 p 是节点 q 的邻居，那么节点 q 也必须是节点 p 的邻居。
图是连通图，你可以从给定节点访问到所有节点。

解题思路：

1. 拷贝所有节点
2. 拷贝所有的边

解题步骤：

1. 深度或广度优先遍历所有的节点
2. 拷贝所有的节点，存储起来
3. 将拷贝的节点，按照原图的连接方法进行连接

复杂度：

深度优先遍历

1. 时间复杂度：O（n）
2. 空间复杂度：O（n）

广度优先遍历

1. 时间复杂度：O（n）
2. 空间复杂度：O（n）

/**
 * // Definition for a Node.
 * function Node(val, neighbors) {
 *    this.val = val === undefined ? 0 : val;
 *    this.neighbors = neighbors === undefined ? [] : neighbors;
 * };
 */

/**
 * @param {Node} node
 * @return {Node}
 */
var cloneGraph = function(node) {
    if(!node){
        return;
    }
    const visited = new Map(); // 记录映射关系
    // 深度优先遍历实现
    const dfs = (node) => {
        // console.log(node.val) // 访问节点
        // 拷贝每一个节点
        const nCopy = new Node(node.val); 
         // 节点存放到已访问, 建立映射关系
        visited.set(node, nCopy);
        (node.neighbors || []).forEach(nodeneighbors=>{
            // 如果没有neighbors 转换成[]
            if(!visited.has(nodeneighbors)){
                dfs(nodeneighbors);
            }
            // 拷贝所有的边
            nCopy.neighbors.push(visited.get(nodeneighbors));
        })
    };
    dfs(node);
    // 给定节点的拷贝 作为对克隆图的引用返回。
    return visited.get(node) 
};

/**
 * // Definition for a Node.
 * function Node(val, neighbors) {
 *    this.val = val === undefined ? 0 : val;
 *    this.neighbors = neighbors === undefined ? [] : neighbors;
 * };
 */

/**
 * @param {Node} node
 * @return {Node}
 */
var cloneGraph = function(node) {
    if(!node){
        return;
    }
    const visited = new Map(); // 记录映射关系
    visited.set(node, new Node(node.val))
    // 广度优先遍历实现
    const queue = [node];
    while(queue.length){
        const n = queue.shift(); // 拿出对头并访问
        // console.log(n.val);
        (n.neighbors || []).forEach(nodeneighbors=>{ 
          // 访问所有邻居节点
            if(!visited.has(nodeneighbors)){
                queue.push(nodeneighbors);
                // 拷贝节点
                visited.set(nodeneighbors, new Node(nodeneighbors.val));
            }
            // 拷贝边
            visited.get(n).neighbors.push(visited.get(nodeneighbors));
        })
    }
    return visited.get(node) // 给定节点的拷贝 作为对克隆图的引用返回。
};

图-章节总结

• 图是网络结构的抽象模型，是一组由边连接的节点
• 图可以表示任何二元关系，比如道路，航班.

技术要点

• JS中没有图，但是可以用Object和Array构件图
• 图的表示法：邻接矩阵，邻接表...
• 图的常用操作：深度、广度优先遍历

思考

1. 用图画出你的朋友圈