数据结构（七）树

树是什么？

一种分层数据的抽象模型
前端工作中常见的树包括：DOM树，级联选择、树形控件
JS中没有树，但是可以用Object和Array构建树
树的常用操作：深度/广度优先遍历、先中后序遍历

什么是树的深度/广度优先遍历？

深度优先遍历：尽可能深的搜索树的分支
广度优先遍历：先访问离根节点最近的节点

深度优先遍历算法口诀

访问根节点

对根节点的children挨个进行深度优先遍历

const tree = {
  val: 'a',
  children: [
    {
      val: 'b',
      children: [
        {
          val: 'd',
          children: []
        },
        {
          val: 'e',
          children: []
        }
        
      ]
    },
    {
      val: 'c',
      children: [
        {
          val: 'f',
          children: []
        },
        {
          val: 'g',
          children: []
        }
      ]
    }
  ]
}

const dfs = (root) => {
  console.log(root.val);
  // root.children.forEach((child)=>{
  //   dfs(child)
  // })
  // 优化写法
  root.children.forEach(dfs)
}
dfs(tree)

广度优先遍历算法口诀

新建一个队列，把根节点入队
把对头出队并访问
把对头的children挨个入队
重复第二三步，知道队列为空

const tree = {
  val: 'a',
  children: [
    {
      val: 'b',
      children: [
        {
          val: 'd',
          children: []
        },
        {
          val: 'e',
          children: []
        }
        
      ]
    },
    {
      val: 'c',
      children: [
        {
          val: 'f',
          children: []
        },
        {
          val: 'g',
          children: []
        }
      ]
    }
  ]
}
const bfs = (root)=>{
  const queue = [root];
  while(queue.length>0){
    const n = queue.shift();
    console.log(n.val)
    n.children.forEach(child=>{
      queue.push(child);
    })
  }
}
bfs(tree)

二叉树的先中后遍历

二叉树是什么？

树中每个节点最多只能有两个子节点
在JS中通常用Object来模拟二叉树

先序遍历算法口诀

访问根节点
对根节点的左子树进行先序遍历
对根节点的右子树进行先序遍历

// 二叉树 bt.js
const bt = {
  val: 1,
  left: {
    val: 2,
    left: {
      val: 4,
      left: null,
      right: null
    },
    right: {
      val: 5,
      left: null,
      right: null
    }
  },
  right: {
    val: 3,
    left: {
      val: 6,
      left: null,
      right: null
    },
    right: {
      val: 7,
      left: null,
      right: null
    }
  }
}
module.exports = bt;

// 先序遍历
const bt = require('./bt');
const preorder = (root)=> {
  if(!root){ return; }
  console.log(root.val)
  preorder(root.left);
  preorder(root.right);
}
preorder(bt);
// 1 2 4 5 3 6 7

中序遍历算法口诀

对根节点的左子树进行中序遍历
访问根节点
对根节点的右子树进行中序遍历

// 中序遍历
const bt = require('./bt');
const inorder = (root)=>{
  if(!root){ return; }
  inorder(root.left);
  console.log(root.val);
  inorder(root.right);
}
inorder(bt)
// 4 2 5 1 6 3 7

后续遍历算法口诀

对根节点的左子树进行后续遍历
对根节点的右子树进行后续遍历
访问根节点

// 后续遍历
const bt = require('./bt');
const postorder = (root)=>{
  if(!root){ return; }
  postorder(root.left);
  postorder(root.right);
  console.log(root.val);
}
// postorder(bt)
// 4 5 2 6 7 3 1

二叉树的先中后序遍历(非递归版)

// 先序遍历（非递归版）核心思路用堆栈，因为在函授中调用另一个函数其实就是连续的调用堆栈，即递归版的原理
const preorderPlus = (root) =>{
  if(!root){ return; }
  const stack = [root];
  while(stack.length){
    const n = stack.pop(); // 最开始访问根节点的值，循环到以后就是部分子树的根节点
    console.log(n.val);
    // 栈：后进先出 所以需要先推right
    if(n.right){// 递归右子树
      stack.push(n.right);
    }
    if(n.left){ // 递归左子树
      stack.push(n.left);
    }
  }
}
preorderPlus(bt)

// 中序遍历（非递归版）
const inorderPlus = (root)=>{
  if(!root){ return; }
  // 核心思路：遍历所有左子树->根节点->右子树
  const stack = [];
  let p = root; // 指针
  while(stack.length || p){ // 循环1,2,3,4
    while(p){
      // 1.把所有子树丢入栈中
      stack.push(p);
      p = p.left;
    }
    // 2.弹出最尽头的节点
    const n = stack.pop();
    // 3.访问最尽头的节点
    console.log(n.val);
    // 4.访问右节点（指针指向右节点）
    p = n.right;
  }
}
inorderPlus(bt)

// 后续遍历（非递归版）
const postorderPlus = (root)=>{
  // 核心思路：
  // 1. 把后续遍历的顺序倒置(左右根->根右左，与先序遍历很像)
  // 2. 把先序遍历的访问操作，改成入栈操作
  // 3. 利用栈的后进先出特性，子节点逆序输出
  if(!root){ return; }
  const outputStack = []; // 做倒置操作的堆栈
  const stack = [root]; // 函数调用堆栈
    while(stack.length){ // 根右左
      const n = stack.pop();
      outputStack.push(n);
      if(n.left){
        stack.push(n.left);
      }
      if(n.right){
        stack.push(n.right);
      }
    }
    while(outputStack.length){ // 倒序输出
      const n = outputStack.pop();
      console.log(n.val);
    }
}
postorderPlus(bt)

LeetCode #104 二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。
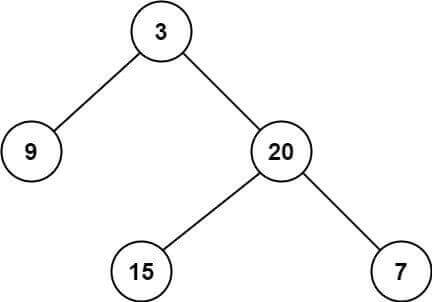
示例：给定二叉树 [3,9,20,null,null,15,7]

返回它的最大深度 3 。

解题思路：

求最大深度，考虑使用深度优先遍历
在深度优先遍历过程中，记录每个节点所在层级，找出最大层级即可。

解题步骤：

新建一个变量记录最大深度
深度优先遍历整棵树，并记录每个节点的层级，同时不断刷新最大深度这个变量。
遍历结束返回最大深度的变量

复杂度：

时间复杂度：O（n）
空间复杂度：最坏 O（n）最好 O（logN）（隐形调用了函数堆栈）

/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    let deepMax = 0;
    const dfs = (node, level)=>{ // level即节点所处层级
        if(!node){
            return;
        }
        if(!node.left && !node.right){ // 只在叶子节点时计算最大深度
            deepMax = Math.max(deepMax, level)
        }
        dfs(node.left, level + 1);
        dfs(node.right, level + 1);
    };
    dfs(root,1);
    return deepMax;
};

LeetCode #111 二叉树的最小深度

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例

输入：root = [3,9,20,null,null,15,7]
输出：2
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

解题思路：

求最小深度，考虑使用广度优先遍历
在广度优先遍历过程中，遇到叶子节点，停止遍历，返回节点层级

解题步骤：

广度优先遍历整颗树，并记录每个节点的层级
遇到叶子节点，返回节点层级，停止遍历

复杂度：

时间复杂度：O（n）
空间复杂度：O（n）

/**
 * @param {TreeNode} root
 * @return {number}
 */
var minDepth = function(root) {
    if(!root) {
        return 0;
    }
    const queue = [[root, 1]]; // 新建队列，并把根节点传入
    while(queue.length){
        const [node, level] = queue.shift(); // 拿出队头，并访问
        if(!node.left && !node.right){ // 如果是叶子节点
            return level
        }
        if(node.left){
            queue.push([node.left, level + 1]); // 当前节点的孩子节点加入对列
        }
        if(node.right){
            queue.push([node.right,level + 1]);
        }
    }
};

LeetCode #102 二叉树的层序遍历

给你一个二叉树，请你返回其按层序遍历得到的节点值。（即逐层地，从左到右访问所有节点）。

示例：
二叉树：[3,9,20,null,null,15,7]

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

解题思路：

层序遍历顺序就是广度优先遍历
不过在遍历时候需要记录当前节点所处的层级，方便将其添加到不同的数组中

解题步骤：

广度优先遍历（用队列）
遍历过程中，记录每个节点的层级，并将其添加到不同的数组中

复杂度：

时间复杂度：O（n）广度优先遍历
空间复杂度：O（n）

/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    if(!root){ // 保证root节点不为空
        return [];
    }
    // 广度优先遍历
    const queue = [[root, 0]]; // 节点，层级
    const res = [];
    while (queue.length) {
        const [node, level] = queue.shift(); // 节点出队，并记录每个节点的层级
        // console.log(node.val, level) // 访问节点
        if(!res[level]){ // res[level]没值的话，先push一个数组
            // 把节点的值按照层级分别push到不同数组，返回
            res.push([node.val])
        }else{
            res[level].push(node.val);
        }
        // 将节点的孩子节点推进队列
        if(node.left){
            queue.push([node.left, level + 1])
        }
        if(node.right){
            queue.push([node.right, level + 1])
        }
    }
    return res;
};

优化方案：

/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    if(!root){ // 保证root节点不为空
        return [];
    }
    const queue = [root];
    const res = [];
    while (queue.length) {
        let len = queue.length;
        res.push([]);
        while(len--){// 优化：保证每次while循环时，老一层级的节点都出队列，其节点的孩子节点们都入队。即保证queue中只有同级节点
            const node = queue.shift();
            res[res.length - 1].push(node.val);
            if(node.left){
                queue.push(node.left)
            }
            if(node.right){
                queue.push(node.right)
            }
        }
    }
    return res;
};

LeetCode #94 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回它的中序遍历。

示例：

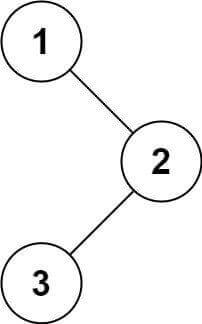
输入：root = [1,null,2,3]
输出：[1,3,2]
输入：root = []
输出：[]
输入：root = [1]
输出：[1]

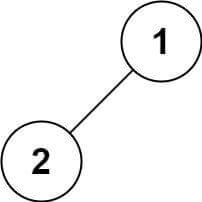
输入：root = [1,2]
输出：[2,1]

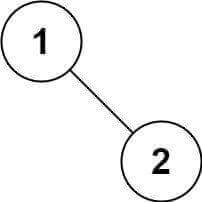
输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
    // 递归版
    const res = [];
    const rec = (node)=>{
        if(!node){
            return;
        }
        // 中序遍历 左根右
        rec(node.left); // 左子树
        res.push(node.val); // 根节点
        rec(node.right); // 右子树
    }
    rec(root);
    return res;
};

优化方案：

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
    // 迭代版
    const res = [];
    const stack = []; // 模拟递归堆栈
    let point = root; // 指针
    while(stack.length || point){ // 整体大循环
        while(point){ // 把所有的左节点推入栈中
            stack.push(point)
            point= point.left;
        }
        const node = stack.pop(); // 访问节点，即出栈
        res.push(node.val);
        point = node.right; // 指针指向右节点
    }
    return res;
};

LeetCode #112 路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例:

给定如下二叉树，以及目标和 sum = 22

       5
      / \
     4   8
    /   / \
  11  13   4
 /  \       \
7    2       1

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

解题思路：

在深度优先遍历的过程中，记录当前路径的节点值的和
在叶子节点处，判断当前路径的节点值的和是否等于目标值

解题步骤：

深度优先遍历二叉树，在叶子节点处，判断当前路径的节点值的和是否等于目标值，是九返回true
遍历结束，如果没有匹配到，就返回false

复杂度：

时间复杂度 O（n）
空间复杂度 O（n）

/**
 * @param {TreeNode} root
 * @param {number} sum
 * @return {boolean}
 */
var hasPathSum = function(root, sum) {
    if(!root){
        return false;
    }
    let res = false;
    const dfs = (node,sumAcc) => {
        // console.log(node.val, sumAcc)
        if(!node.left && !node.right && sumAcc === sum){
            res = true;
        }
        if(node.left){
            dfs(node.left, sumAcc + node.left.val)
        }
        if(node.right){
            dfs(node.right, sumAcc + node.right.val)
        }
    }
    dfs(root, root.val);
    return res;
};

前端与树：遍历JSON的所有节点值

用途：清洗JSON

const json = {
  a: { b: { c: 1 } },
  d: [1, 2]
}

const dfs = (node, path) => {
  console.log(node, path); // 访问当前节点
  Object.keys(node).forEach(k=>{ // 获取所有key，即所有孩子节点
    dfs(node[k], path.concat(k));
  })
}

dfs(json, []);

前端与树：渲染Antd的树组件

// CodePen 模拟树组件
const {  Tree  } = antd;

const { TreeNode } = Tree;

const json = [
  {
    title: "一",
    key: "1",
    children: [{title:"三",key:"3",children:[
     {title:"五",key:"5",children:[]} 
    ]}]
  },
  {
    title: "二",
    key: "2",
    children: [{title:"四",key:"4",children:[]}]
  },
]

class Demo extends React.Component {
  dfs = (node)=>{
    return (
      <TreeNode title={node.title} key={node.key}>
        {node.children.map(this.dfs)}
      </TreeNode>
    )
  }
  render() {
    const tProps = {
      treeDefaultExpandAll: true,
      style: {
        width: '100%',
      },
    };
    return (
      <Tree {...tProps}>
        {json.map(this.dfs)}
      </Tree>
    );
  }
}

ReactDOM.render(<Demo />, mountNode);

树-总结

树是一种分层数据的抽象模型，在前端广泛应用
树的常用操作：深度、广度优先遍历，先中后序遍历...

数据结构（七）树

数据结构（七）树

树是什么？

什么是树的深度/广度优先遍历？

深度优先遍历算法口诀

广度优先遍历算法口诀

二叉树的先中后遍历

二叉树是什么？

先序遍历算法口诀

中序遍历算法口诀

后续遍历算法口诀

二叉树的先中后序遍历(非递归版)

LeetCode #104 二叉树的最大深度

LeetCode #111 二叉树的最小深度

LeetCode #102 二叉树的层序遍历

LeetCode #94 二叉树的中序遍历

LeetCode #112 路径总和

前端与树：遍历JSON的所有节点值

前端与树：渲染Antd的树组件

树-总结

数据结构（八）图

数据结构（六）字典

xuhao

Comments | NOTHING

树是什么？

什么是树的深度/广度优先遍历？

深度优先遍历算法口诀

广度优先遍历算法口诀

二叉树的先中后遍历

二叉树是什么？

先序遍历算法口诀

中序遍历算法口诀

后续遍历算法口诀

二叉树的先中后序遍历(非递归版)

LeetCode #104 二叉树的最大深度

LeetCode #111 二叉树的最小深度

LeetCode #102 二叉树的层序遍历

LeetCode #94 二叉树的中序遍历

LeetCode #112 路径总和

前端与树：遍历JSON的所有节点值

前端与树：渲染Antd的树组件

树-总结

数据结构（八）图

数据结构（六）字典

xuhao

Comments | NOTHING

你想搜索什么...