一、背景

在去年年底的时候，我的项目组开始了对于直播教学的开发和技术预研。我们都知道，直播教学中涉及到音频信号，视频信号，信令，以及师生笔记（Canvas的巨量Path数组）。因为在进行代码review的时候，我发现了，对于我们的实时师生笔记交互，信令因为也是实时传送的，因此会很高频，有时甚至遇到超频的问题被限制频率。所以我再想是不是可以对实时笔记的路径进行抽稀，这样我们传送的信令是不是就没那么多了。举例老师写了一个高中数学的公式，这个公式的JSON序列化队列假设是一个9000条的数组矩阵集合，那么我们运用抽稀算法，可以抽取其中的一些，是不是传送的信令就会变得少啦？性能是不是也就上来了？哈哈。等等，别急！！这个时候，有个问题我们应该注意了，就是你会疑惑抽稀以后笔记会不会失真呢？因为我们知道笔记的抽象就是和微积分的原理一样的，可以抽象为多个线段的集合拼接而成。因此如果没有章法的抽稀，势必会失真，那我们的优化也就失去了意义，不是吗？

二、解决方案

方案一：
这个时候我们可以想到著名的数学家D.Douglas和T.Peueker于1973年提出的道格拉斯—普克(Douglas一Peukcer)节点抽稀算法，简称D-P算法。
现有的线化简算法中，有相当一部分都是在该算法基础上进行改进产生的。它的长处是具有平移和旋转不变性，给定曲线与阂值后，抽样结果一定。本章线化简重点解说该算法。
算法的基本思路是: 对每一条曲线的首末点虚连一条直线,求所有点与直线的距离,并找出最大距离值dmax ,用dmax与限差D相比:若dmax < D ,这条曲线上的中间点所有舍去;若dmax ≥D ,保留dmax 相应的坐标点,并以该点为界,把曲线分为两部分,对这两部分反复使用该方法。

算法的具体过程如下:
(1) 在曲线首尾两点间虚连一条直线,求出其余各点到该直线的距离，如图3（1）。
(2) 选其最大者与阈值相比較,若大于阈值,则离该直线距离最大的点保留,否则将直线两端点间各点所有舍去，如图3（2），第4点保留。
(3) 根据所保留的点,将已知曲线分成两部分处理,反复第1、2步操作，迭代操作，即仍选距离最大者与阈值比較,依次取舍,直到无点可舍去，最后得到满足给定精度限差的曲线点坐标，如图3（3）、（4）依次保留第6点、第7点，舍去其它点,即完成线的化简。

方案二：
当我实现了第一种道格拉斯抽稀算法时，与我的项目结合完成时，我的脑子里灵光一现，好想有另一种方案。不知道大家还记得不记得我们上高中学习的等差数列。对等差数列的思路就是核心，抽象方法就是，进行整个线段的间隔性抽稀。就是下方CODE中的公差（抽稀程度）。举个例子，就是一条线段有100个点，我每隔4个点就抽取的话，就可以尽可能保证保真度的情况下进行抽稀动作。不得不承认，我比不过D.Douglas和T.Peueker两位老前辈

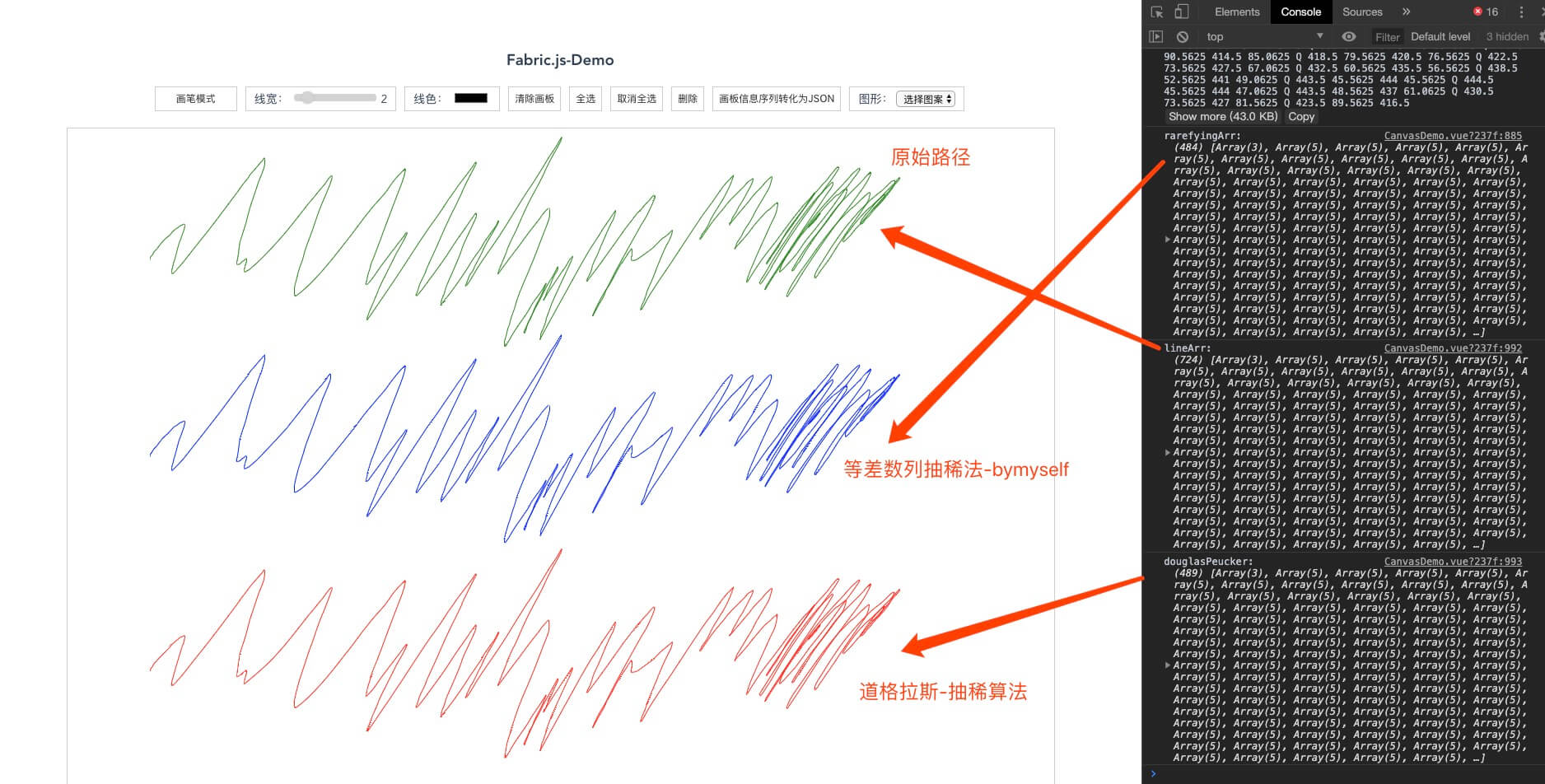
三、这就是无抽稀，道格拉斯抽稀，等差抽稀三种情况下的对比效果图

四、代码实现（关于此篇文章，会后续继续完善，有很多想说的，相对比的还有待继续呈现...）

/*
 * @Author: xuhao 
 * @Date: 2019-12-30 15:01:14 
 * @Last Modified by: xuhao
 * @Last Modified time: 2020-03-09 00:56:41
 */

/*
* Desc: Performance Optimize For Live Class
* Function List: 
*    1.Arithmetic Progression Diluting Algorithm for Free Draw Path
*    2.Douglas Peucker Diluting Algorithm for Free Draw Path
*/

/*
 * 表现说明：目前来看，一般抽稀程度，等差数列抽稀算法所表现的抽稀后的轨迹更加清晰圆润，后期会继续优化。
 * 但极限抽取情况下，道格拉斯抽稀算法更胜一筹，总体轨迹不损。
*/

// 多维数组扁平化
const reduceDimension = (arr) => {
  return Array.prototype.concat.apply([], arr);
}

/*** 等差数列抽稀算法 Arithmetic-Progression-Diluting-Algorithm（creat by: xuhao）***/
// 数组等差分割函数【按（公差，即抽稀程度）进行）】
const splitArray = (tolerance, arr) => {
  let list = [],
    index;
  for (index = 0; index < arr.length;) {
    list.push(arr.slice(index, (index += tolerance)));
  }
  return list;
};

// 抽稀
const diluting = (arr) => {
  let vacuateArr = [];
  for (let i = 0; i < arr.length; i++) {
    let itemLen = arr[i].length;
    vacuateArr.push(arr[i][0]);
    // if(i!=0){
    //   vacuateArr.push(arr[i][Math.ceil((0+itemLen)/2)]);
    // }
    vacuateArr.push(arr[i][itemLen - 1]);
  }
  return vacuateArr;
};

/**
 *@param arr 原始轨迹Array
 *@param tolerance 抽稀程度系数，即 2/tolerance
 *@return rarefyingArr 抽稀后的轨迹
 */
// 等差数列抽稀 入口函数（后续会继续优化，取点算法）
const apDiluting = (arr, tolerance = 3) => {
  let arithmeticArr = splitArray(tolerance, arr);
  let rarefyingArr = diluting(arithmeticArr);
  return rarefyingArr;
}

/*** 道格拉斯-抽稀算法 Douglas-Peuker-Algorithm ***/
// 计算两点之间的距离
const calculationDistance = (point1, point2) => {
  // longitude，经度，即x轴上的值
  // latitude，纬度，即y轴上的值
  let lat1 = point1[point1.length - 1];
  let lat2 = point2[point2.length - 1];
  let lng1 = point1[1];
  let lng2 = point2[1];
  let radLat1 = (lat1 * Math.PI) / 180.0;
  let radLat2 = (lat2 * Math.PI) / 180.0;
  let a = radLat1 - radLat2;
  let b = (lng1 * Math.PI) / 180.0 - (lng2 * Math.PI) / 180.0;
  let s =
    2 *
    Math.asin(
      Math.sqrt(
        Math.pow(Math.sin(a / 2), 2) +
        Math.cos(radLat1) *
        Math.cos(radLat2) *
        Math.pow(Math.sin(b / 2), 2)
      )
    );
  return s * 6370996.81;
};

// 计算点pX到点pA和pB所确定的直线的距离
const distToSegment = (start, end, center) => {
  let a = Math.abs(calculationDistance(start, end));
  let b = Math.abs(calculationDistance(start, center));
  let c = Math.abs(calculationDistance(end, center));
  let p = (a + b + c) / 2.0;
  let s = Math.sqrt(Math.abs(p * (p - a) * (p - b) * (p - c)));
  return (s * 2.0) / a;
};

// 递归方式压缩轨迹
const compressLine = (coordinate, result, start, end, dMax) => {
  if (start < end) {
    let maxDist = 0;
    let currentIndex = 0;
    let startPoint = coordinate[start];
    let endPoint = coordinate[end];
    for (let i = start + 1; i < end; i++) {
      let currentDist = distToSegment(startPoint, endPoint, coordinate[i]);
      if (currentDist > maxDist) {
        maxDist = currentDist;
        currentIndex = i;
      }
    }
    if (maxDist >= dMax) {
      //将当前点加入到过滤数组中
      result.push(coordinate[currentIndex]);
      //将原来的线段以当前点为中心拆成两段，分别进行递归处理
      compressLine(coordinate, result, start, currentIndex, dMax);
      compressLine(coordinate, result, currentIndex, end, dMax);
    }
  }
  return result;
};

// 道格拉斯-抽稀 入口函数
/**
 *@param coordinate 原始轨迹Array
 *@param dMax 允许最大距离误差
 *@return douglasResult 抽稀后的轨迹
 */
const douglasPeucker = (coordinate, dMax = 10) => {
  if (!coordinate || !(coordinate.length > 2)) {
    return null;
  } else {
    coordinate.forEach((item, index) => {
      item['id'] = index;
    });
  }
  let result = compressLine(coordinate, [], 0, coordinate.length - 1, dMax);
  result.push(coordinate[0]);
  result.push(coordinate[coordinate.length - 1]);
  let resultLatLng = result.sort((a, b) => {
    if (a.id < b.id) {
      return -1;
    } else if (a.id > b.id) return 1;
    return 0;
  });
  resultLatLng.forEach(item => {
    item.id = undefined;
  });
  return resultLatLng;
};

export default {
  apDiluting,
  douglasPeucker,
  reduceDimension
}

参考文献