什么是树的深度/广度优先遍历？

• 深度优先遍历：尽可能深的搜索树的分支
• 广度优先遍历：先访问离根节点最近的节点

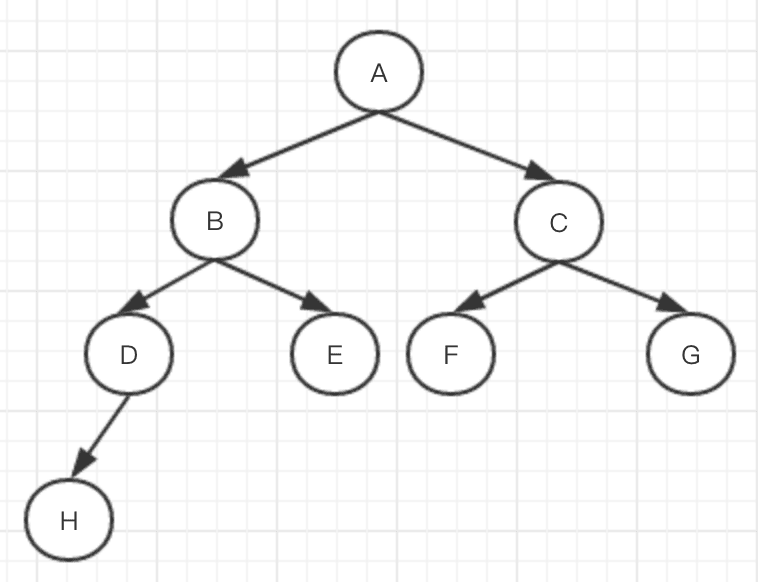
• 深度优先遍历，如上图所示，会先访问根节点A，然后沿着左树一直向下深层访问遍历，即A-B-D-H-E-C-F-G
• 广度优先遍历，如上图所示，会先访问根节点A，然后向下一层，并将该层访问遍历完毕，再继续向下一层遍历。即A-B-C-D-E-F-G-H

深度优先遍历算法

• 访问根节点
• 对根节点的children挨个进行深度优先遍历

const tree = {
 val: 'a',
 children: [
   {
     val: 'b',
     children: [
      {
       val: 'd',
       children: []
      },
      {
       val: 'e',
       children: []
      }  
     ]
   },
   {
     val: 'c',
     children: [
      {
        val: 'f',
        children: []
      },
      {
        val: 'g',
        children: []
      }
     ]
   }
 ]
}

const dfs = (root) => {
  console.log(root.val);
  // root.children.forEach((child)=>{
  //   dfs(child)
  // })
  // 优化写法
  root.children.forEach(dfs)
}
dfs(tree)
// a b d e c f g

广度优先遍历算法

• 新建一个队列，把根节点入队
• 把对头出队并访问
• 把对头的children挨个入队
• 重复第二三步，知道队列为空

const tree = {
  val: 'a',
  children: [
    {
      val: 'b',
      children: [
        {
          val: 'd',
          children: []
        },
        {
          val: 'e',
          children: []
        }
        
      ]
    },
    {
      val: 'c',
      children: [
        {
          val: 'f',
          children: []
        },
        {
          val: 'g',
          children: []
        }
      ]
    }
  ]
}
const bfs = (root)=>{
  const queue = [root];
  while(queue.length>0){
    const n = queue.shift();
    console.log(n.val)
    n.children.forEach(child=>{
      queue.push(child);
    })
  }
}
bfs(tree)
// a b c d e f g